- 2021.03.16(화) 추가
faculty.cs.niu.edu/~freedman/340/340notes/340hash.htm
Hashing
Hashing Hashing can be used to build, search, or delete from a table. The basic idea behind hashing is to take a field in a record, known as the key, and convert it through some fixed process to a numeric value, known as the hash key, which represents the
faculty.cs.niu.edu
위 사이트에는 아래 글에서 소개할
두 가지 간단한 충돌 처리 방식 외에
두 가지 심화 버전의 충돌 처리 방식을 소개한다.
더불어, 간단한 수도 코드도 있으며
설명이 영어로 적혀 있긴 해도 해석하는데 큰 어려움이 없을 정도의 난이도라
읽어보면 좋을 듯 싶다.
지난 글에서 해시에 대해 간략하게 살펴보았다.
이번 글에서는 해시를 이용하는 자료구조 중
'해시 테이블'과 해시 값 충돌 시 처리 방식에 대해
자세히 알아본다.
해시 테이블 - 정의
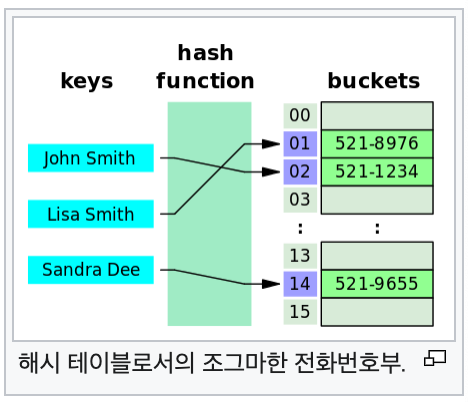
위 그림처럼 해시 값을 키(key)로 사용하여
데이터에 접근할 수 있는 자료구조를
'해시 테이블'이라 한다.
C든 Python이든 언어마다 '배열'이라는
자료구조가 존재하는데,
이 '배열'은 인덱스만 안다면
해당 인덱스에 존재하는 데이터의 조회 시간은 상수 시간이 된다.
그래서 해시 함수를 사용하여 얻은 해시 값을
어떠한 데이터를 찾을 때 인덱스로 사용하면,
정렬을 하지 않고도 빠른 검색, 빠른 삽입이 가능하게 된다..
물론 충돌이 없는 경우!
(단, '해시 테이블'과 유사한 목적으로 사용하는 해시 함수는
해시 값을 계산하는 비용이 기존 검색 알고리즘에 비해 훨씬 적고
뛰어나야 한다는 전제 조건이 붙는다)
그러나 서로 다른 입력 키 값이 동일한 해시 값,
즉, 인덱스로 매핑될 경우 해시 충돌이 발생하여
성능을 떨어뜨리게 된다.
해시 분포와 해시 충돌
해시 충돌이 발생했을 경우 처리 방식에 대해 알아보기 전에,
잠깐 해시에 대해 더 자세히 알아보자.
어려운 내용이니 집중이 필요하다!
[해시 분포]
서로 다른 객체 X, Y가 있을 때,
즉, X.equals(Y)가 '거짓'일 때
X.hashCode()와 Y.hashCode()가 같지 않다면,
이때 사용된 해시 함수는 '완전한 해시 함수(perfect Hash Function)'라고 한다.
Boolean처럼 구별 가능한 객체의 종류가 적거나,
Interger, Long, Double 같은 Number 객체는
객체가 나타내려는 값 자체를 해시 값으로 사용할 수 있기 때문에
완전한 해시 함수라고 할 수 있다.
하지만 String이나 POJO(Plain Old Java Object)에 대해
완전한 해시 함수를 만드는 것은 사실상 불가능하다.
[해시 충돌]
HashMap처럼 해시 함수를 이용하는 Associative Array 구현체(Wiki 링크)에서는
메모리를 절약하기 위해 실제 해시 함수의 표현 범위 N보다 작은
M개의 원소가 있는 배열(해시 버킷)만을 사용하는데,
이유는 아래와 같다.
이유를 설명하기 위해 HashMap을 예로 들어 알아보자.
만약 적은 연산만으로 빠르게 동작 가능한 완전한 해시 함수가 있어도,
그것을 HashMap에서 사용할 수 있지는 않다.
왜냐하면 HashMap은 기본적으로
각 객체의 hashCode() 메서드가 반환하는 값을 Key 값으로 사용하는데,
hashCode() 메서드가 return하는 자료형은 int다.
즉, 32비트 정수 자료형인데,
이것으로는 완전한 자료 해시 함수를 만들 수 없다.
이유는,
(1) 논리적으로 생성 가능한 객체의 수가 2^32보다 많을 수 있기 때문이며,
(2) 모든 HashMap 객체에서 O(1)을 보장하기 위해 랜덤 접근이 가능하게 하려면
원소가 2^32인 배열을 모든 HashMap이 갖고 있어야 하기 때문이다.
따라서 아래처럼 객체에 대한 hashCode()의 나머지 값을
해시 버킷 인덱스 값으로 사용한다.
int index = X.hashCode() % M;
위와 같은 방식을 사용하면,
서로 다른 해시 코드를 가지는
서로 다른 객체가 1/M의 확률로
같은 해시 버킷 인덱스를 사용하게 된다.
이는 해시 함수가 얼마나 해시 충돌을 회피하도록
잘 구현되었느냐에 상관없이 발생할 수 있는
또 다른 종류의 해시 충돌이다.
이렇게 해시 충돌이 발생했을 때,
Key-Value 쌍 데이터를 잘 저장하고 조회할 수 있게 하는 방식에는
대표적으로 아래 두 가지 방식이 있다.
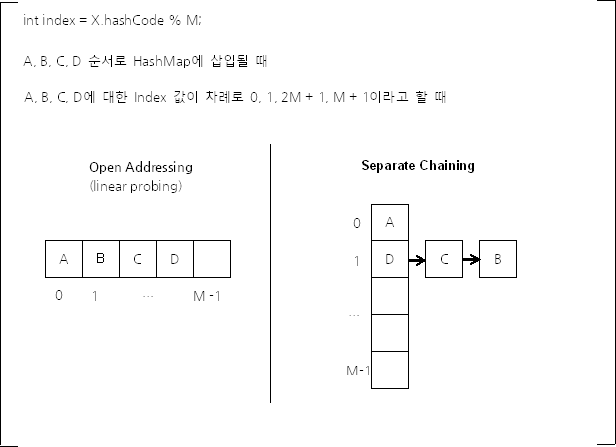
충돌 처리 방식
Separate Chaining(개별 체이닝)
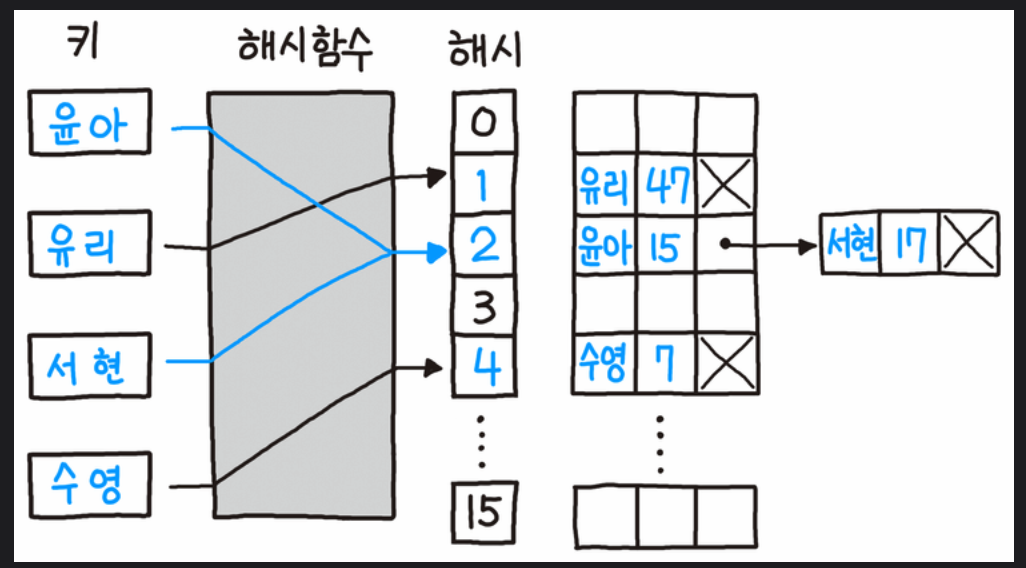
해시 테이블의 기본 방식이기도 한
개별 체이닝(Seperate Chaining)은
충돌이 발생하면 그림처럼 연결 리스트(linked list)로
연결하는 방식이다.
위 그림에서는 '윤아'와 '서현'의 해시 값이 같기 때문에,
먼저 들어온 '윤아' 뒤에 '서현'을 연결 리스트의 형태로 붙여
데이터를 유지한다.
이처럼 기본적인 자료구조와
임의로 정한 간단한 알고리즘만 있으면 되므로,
개별 체이닝 방식은 인기가 높다.
원래 해시 테이블 구조의 원형이기도 하며
가장 전통적인 방식으로,
흔히 해시 테이블이라고 하면 이 방식을 말한다.
Open Addressing(오픈 어드레싱)
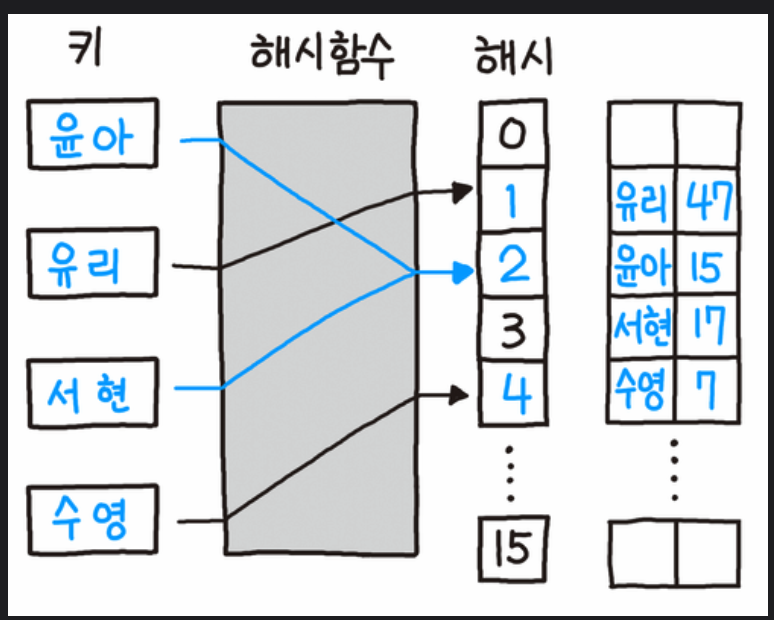
오픈 어드레싱(Open Addressing) 방식은
충돌이 발생하면 그림처럼 탐사(Probing)를 통해
빈 공간을 찾아 데이터를 저장한다.
(그림은 가장 간단한 방식인
선형 탐사-Linear Probing-방식이며,
충돌이 발생하면 해당 위치부터 순차적으로 하나씩 탐사를 진행한다,
선형 탐사 방식은 구현 방법이 간단하면서도
의외로 전체적인 성능이 좋은 편이다)
위 그림에서는 '윤아'와 '서현'의 해시 값이 '2'로 동일하여
충돌이 발생하자,
다음 빈 공간인 '3'에 '서현'이 들어가게 되었다.
그래서 체이닝 방식과 달리,
모든 데이터가 반드시 자신의 해시 값과 일치하는 주소에
저장된다는 보장은 없다.
또한 체이닝 방식은 사실상 데이터를 무한정 저장할 수 있지만,
오픈 어드레싱 방식은 정해진 해시 버킷의 개수 이상은 저장할 수 없다.
Separate Chaining(개별 체이닝) vs Open Addressing(오픈 어드레싱)
두 방식 모두 Worst Case는 O(N)이지만,
Open Addressing은 연속된 공간에 데이터를 저장하기 때문에
Seperate Chaining에 비하여 캐시 효율이 높다.
따라서 데이터 개수가 충분히 적다면,
Open Addressing이 Seperate Chaining보다 더 성능이 좋지만,
배열의 크기가 커질수록(N 값이 커질수록, 즉 HashTable의 크기가 커질수록)
L1, L2 캐시 적중률(Hit Ratio)가 낮아지기 때문에
Open Addressing의 캐시 효율 장점은 사라진다.
또한, Seperate Chaining이 Open Addressing보다 더 빠른 이유를 알아보기 위해
실제로 자주 쓰이는 Java의 HashMap을 예로 들어보자.
Open Addressing은 데이터를 삭제하려면 효율적으로 처리하기 어렵기 때문에
HashMap의 remove()와 같은 삭제 메서드가 매우 빈번하게 호출되며,
HashMap에 저장된 Key-Value 쌍 개수가 일정 개수 이상으로 많아지면,
일반적으로 Open Addressing은 Seperate Chaining보다 느리다.
Open Addressing의 경우 해시 버킷(해시 테이블)을 채운 밀도가 높아질수록
Worst Case 발생 빈도가 더 높아지기 때문이다.
반면 Seperate Chaining 방식의 경우,
해시 충돌이 잘 발생하지 않도록 조정할 수 있다면
Worst Case 또는 Worst Case에 가까운 일이 발생하는 것을 줄일 수 있다.
해시 테이블 - 충돌 처리 방식 성능
이렇게 충돌 해결을 해도
결과적으로 충돌로 인한 성능 저하는 막을 수 없다.
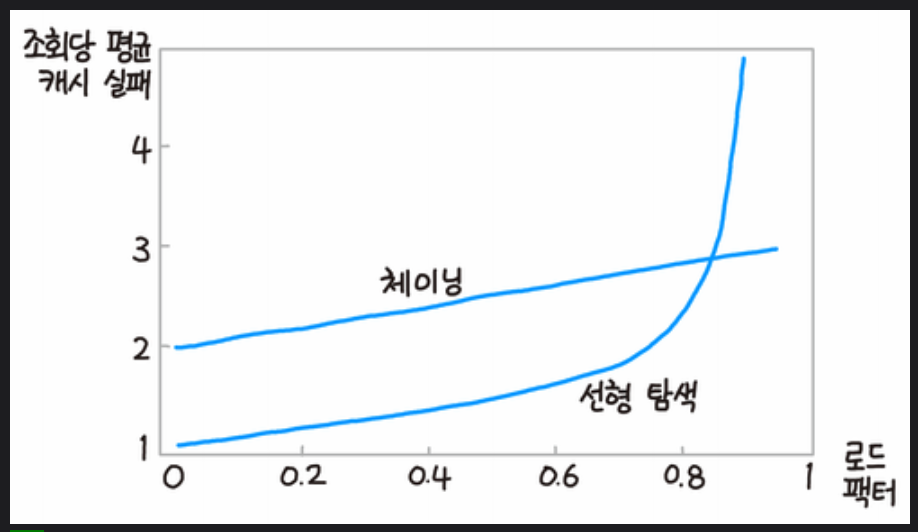
위 그림처럼 수용률이 일정량을 넘어서게 되면
저장, 조회 성능이 모두 점점 떨어진다.
그래서 수용률이 일정량을 넘어가게 되는 경우에는
다음의 방식들을 사용한다.
첫 번째로,
아예 리스트(해시 버킷) 자체의 크기를 키운 뒤에 재배열 하는 방법을 사용한다.
다만, 그러한 재배열 과정 자체가
상당히 비용이 많이 드는 과정이라서
실시간으로 빠르게 처리해야 되는 환경에서는 무리가 있을 수 있다.
그래서 두 번째 방법으로는,
큰 리스트를 하나 더 만들어서
적당한 타이밍에 몇 개씩 점진적으로 옮기다가
다 옮기면 기존의 테이블을 없애 확장하는 방식도 있다.
다만, 이 경우에는 데이터를 옮기는 것 때문에
메모리를 훨씬 더 많이 사용하게 된다.
아니면 세 번째 방법으로,
해시의 bit 수를 늘리는 방법도 있다.
항목 수가 적을 때에는
짧은(적은 bit 수) 해시와 작은 저장공간을 사용하다가,
충돌이 잦아지면
bit 수를 1bit 늘리고 저장공간도 2배로 늘린다.
그리고 항목을 점진적으로 확장된 공간으로
이전하게 함으로써 충돌을 줄일 수 있는 방식인데,
이를 'Consistent hasing' 이라고 부르며
분산 데이터베이스에서 데이터의 일관성을
유지하기 위해 사용되고 있다.
해시 테이블 - 각 언어별 구현 방식
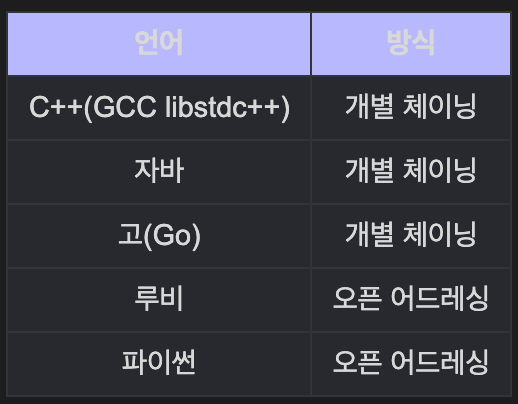
다음 글에서는 보안과 해시에 대해 알아보며
해시 글을 마치려고 한다.
끝!
'Study > Data Structure' 카테고리의 다른 글
| [자료구조] 해시(Hash)란? - (3) 보안 (0) | 2021.03.14 |
|---|---|
| [자료구조] 해시(Hash)란? - (1) 개념, 충돌, 예시, 알고리즘 (0) | 2021.03.14 |
