거의 모든 DBMS는 인덱스 종류에 대해 특별한 언급이 없다면,
B-Tree 계열 인덱스를 사용하는 경우가 대다수이다.
많고 많은 자료구조에서 왜 하필 B-Tree, B+-Tree를 사용하는지에 대해 알아본다.
이 글을 읽기 전에 이전 글을 읽고 오면 좋으며, 아래 사이트들의 내용을 토대로 작성했다.
- [Naver D2] 성능 향상을 위한 SQL 작성법
- [Tistory] 데이터베이스 인덱스는 왜 'B-Tree'를 선택하였는가
- [Tistory] 인덱스(index)란?
- [Tistory] B-Tree(B트리), B+트리
Tree란?
이 글을 찾아왔다는 것 자체가 Tree에 대한 개념은 이미 알고 있을 것이라 생각하고,
먼저 시간 복잡도에 대해 생각해보자.
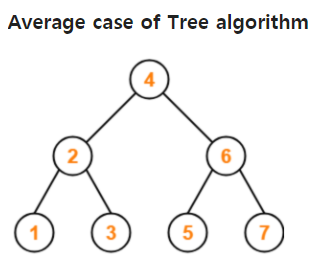
일반적으로 위의 그림처럼 평균적으로 생긴 Tree에서 탐색에 대한 시간 복잡도는
O(log N)이다,

하지만, 위의 그림처럼 Tree의 형태가 한쪽으로 추욱 늘어진 최악의 경우엔
O(N)이다.
이러한 최악의 경우를 대비해서 Balanced Tree라는 것을 사용한다.
Balanced Tree?
말 그대로 "균형잡힌 Tree"로,
위에서 본 Tree 구조의 최악의 경우처럼,
트리가 한쪽으로 쏠리지 않게 노드 삽입 및 삭제 시에 특정 규칙에 따라 트리가 재정렬되어
좌 / 우 SubTree의 밸런스를 유지하는 Tree이다.
항상 좌 / 우 SubTree 간에 밸런스를 유지하고 있기 때문에
탐색에 대한 시간 복잡도는 언제나 O(log N)이지만,
노드 삽입 및 삭제 시 발생하는 재정렬 작업 때문에
탐색을 제외한 작업에서는 일반 Tree보다 성능이 좋지 않다.
이러한 Balanced Tree의 예시에는 AVL-Tree, RedBlack-Tree, B-Tree 등이 있다.
왜 하필 (Balanced) Tree를?
Balanced Tree는 최악의 경우에도 탐색 시간이 O(log N)이므로,
탐색 기능 자체만 봤을 때에는 효율적인 자료구조임을 알 수 있다.
하지만 이전 글에서 Hash에 대해 공부하며,
Hash Table이라는 자료구조는 (평균적으로) 모든 자료구조 중 가장 빠른 탐색 시간인
O(1)을 가지는 것을 배웠다.
그렇다면 왜 Hash Table을 쓰지 않고 Balanced Tree를 쓸까?
DB 인덱스가 빠른 데이터 조회를 위해 사용하는 것이라면,
Hash Table을 사용하는 것이 더 효율적인 것 아닐까?
Hash Table의 치명적 단점
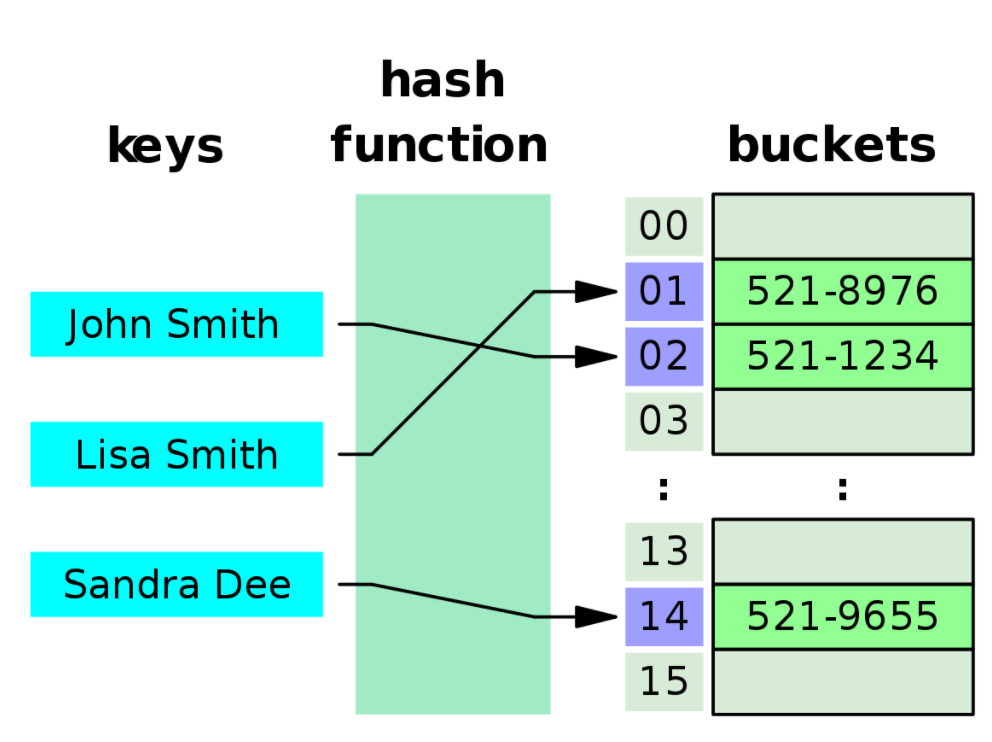
Hash Table을 DB 인덱스로 사용할 수 없는 이유에 대해 알아보기 전에
간단하게 개념 먼저 복습하자.
Hash Table은 Hash Function이라는 특정 계산을 하는 함수에 입력 값(keys)이 들어오면
언제나 같은 결과 값(Hash 값)을 내뱉는다.
그리고 이 결과 값은 Hash Table(buckets)의 index 값으로 매핑되어 찾고자 하는 데이터를 얻을 수 있고,
이 과정은 미리 저장된 메모리 공간(Hash Table)에 한 번에 접근을 하기 때문에
O(1)이라는 어떠한 자료구조나 알고리즘보다 빠른 탐색 시간을 갖게 된다.
(물론 Hash 값이 충돌이 일어나는 등의 최악의 경우, O(N)이 될 수도 있다)
이러한 Hash Table의 동작 원리를 머리에 담고,
우리가 DB를 사용할 때 어떤 방식으로 데이터를 조회하는지 생각해보자.
Select CustomerName From Customer Where CustomerID = '2'
위 SQL 쿼리문처럼 조건에 등호(=)만 써서 데이터를 조회했던가?
아니다, "Where CustomerID >= '2'"처럼 부등호도 사용한다.
오히려 이처럼 특정 범위의 값을 조회하는 일이 더 많을 수도 있다.
다시 Hash Table로 돌아오면,
O(1)이라는 탐색 시간은 "단 하나의 데이터를 탐색하는 시간"이다.
그리고 Hash Table에 저장되는 값들은 정렬되어 있지 않기 때문에
특정 값보다 크거나 작은 값을 찾을 수 없다.
혹여 찾을 수 있다 하더라도 O(1) 보다 더 오랜 시간이 걸릴 것이다.
이러한 이유 때문에 DB 인덱스의 자료구조로 Hash Table은 매우 비효율적이어서 잘 사용하지 않고,
Balanced Tree를 사용한다.
그럼 다른 Balanced Tree나 자료구조는?
글 초반부에 Balanced Tree에 대해 설명하며 RedBlack-Tree와 B-Tree를 언급했었다.
두 트리 모두 Balanced Tree이기 때문에
최악의 경우에도 데이터 탐색 시간 O(log N)을 보장하는데,
왜 RedBlack-Tree는 DB 인덱스의 자료구조가 되지 못했을까?
해당 이유에 대해 알아보기 전에 두 트리가 어떤 것인지 간단하게 살펴보자.
RedBlack-Tree?
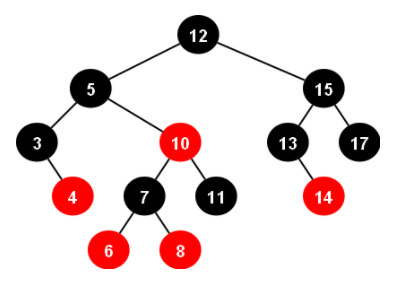
RedBlack-Tree는 위 그림처럼 각 노드(node)가 하나의 데이터만 가진 상태로
좌 / 우 SubTree의 밸런스를 유지한다.
빨간색(Red)과 검은색(Black) 노드로 구분 지어
노드의 삽입 및 삭제 작업 시, 정해둔 규칙들에 맞게 노드들을 재 정렬하며
AVL-Tree보다는 약간 완화된 버전으로 생각하면 된다.
(더욱 자세한 설명은 위키백과의 글을 참고)
B-Tree?
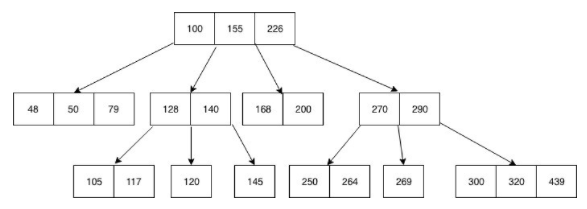
B-Tree는 위처럼 하나의 노드에 여러 데이터가 저장 가능한 트리이며,
Root - Branch - Leaf의 형태를 갖고 있다.
노드 내의 데이터들은 항상 정렬된 상태이며,
해당 데이터들 사이의 범위를 이용하여 자식 노드를 가질 수 있기 때문에
노드 내 데이터의 개수가 N개일 때, 자식 노드의 개수는 (N + 1) 개다.
DB 인덱스를 B-Tree로 구성할 경우,
가장 아래의 Leaf Node에 인덱스 Value에 대한 RowID를 저장한다.
(TMI)
인덱스를 구성하는 컬럼의 Cardinality가 높은 경우, 즉, 중복된 값의 Row가 적은 비율을 가지는 컬럼,
다시 말해, 컬럼의 분포도가 10~15% 이내인 경우 적합하다.
RedBlack-Tree의 치명적 단점
위 그림들만 봐도 알 수 있듯이,
RedBlack-Tree와 B-Tree의 가장 큰 차이는 '하나의 노드 내의 데이터 개수'이다.
RedBlack-Tree는 하나의 노드 내에 무조건 하나의 데이터만을,
B-Tree는 하나의 노드 내에 여러 데이터를 저장할 수 있다.
이러한 데이터 저장 방식의 차이는 어떤 차이를 일으킬까?
바로 "데이터 탐색 시의 속도 차이"다.
Tree 자료구조에서 데이터를 탐색할 때에는,
가장 위에 있는 root 노드부터 시작하여 찾는 데이터가 나올 때까지
자식 노드로 내려가며 탐색한다.
RedBlack-Tree의 구조를 보면 하나의 노드에 하나의 데이터만 있기 때문에
자식 노드로 넘어가는 횟수가 많을 것이고,
그러한 노드와 노드 사이는 "참조 포인터(reference pointer)"로 연결되어 있다.
하지만 B-Tree의 경우,
하나의 노드 내에 정렬된 데이터들이 마치 "배열"의 모습을 띄고 있는데
실제 메모리 상에 배열처럼 차례대로 저장이 되어있다.
컴퓨터 공학 관련 과목이나 공부를 해본 사람이라면,
포인터로 메모리에 접근 시 CPU 연산을 통해 주소를 알아내는 등의 부가적인 연산이 필요하기 때문에
실제 메모리 디스크에서 바로 다음 인덱스로 접근을 하는 배열 방식이
포인터 접근을 하는 것보다 훨~씬 빠르다는 것을 알 것이다.
물론, 이론적인 시간 복잡도는 두 트리 모두 O(log N)이지만
위와 같은 물리적인 메모리 처리에서 퍼포먼스 차이는 배열 구조의 접근 방식이 굉장히 빠를 수밖에 없다.
데이터 개수가 무의미할 정도로 적다면 상관없겠지만,
유의미할 정도로 많은 개수를 다룬다면 큰 차이가 있을 것이다.
(참고 - B-Tree 시간 복잡도 계산)
B-Tree에서 시간 복잡도를 계산할 때,
노드들 간 탐색 시간인 O(log N)과 하나의 노드 내 데이터를 탐색하는 시간인 O(log M)을
따로 계산해야 하는지 의문이 생길 수 있다.
하지만, 일반적으로 B-Tree는 하나의 노드에 저장될 노드 개수를 상수로 제한하기 때문에
시간 복잡도 계산에서 제외된다.
그럼 배열을 쓰면 되지 않나?
RedBlack-Tree를 사용하지 않는 이유가 포인터 접근 방식으로 인한 속도 이슈 때문이라면,
아예 배열을 DB 인덱스로 사용하면 되지 않을까?
응, 아니다.
배열의 치명적 단점

배열에 대한 설명은 최근 올라온 유튜브 영상(링크)으로 대체한다.
노마드 코더로 유명한 니콜라스 님의 12분짜리 배열 설명 영상인데
말씀하시는 속도가 느려서 2배속으로 봐도 충분하다.
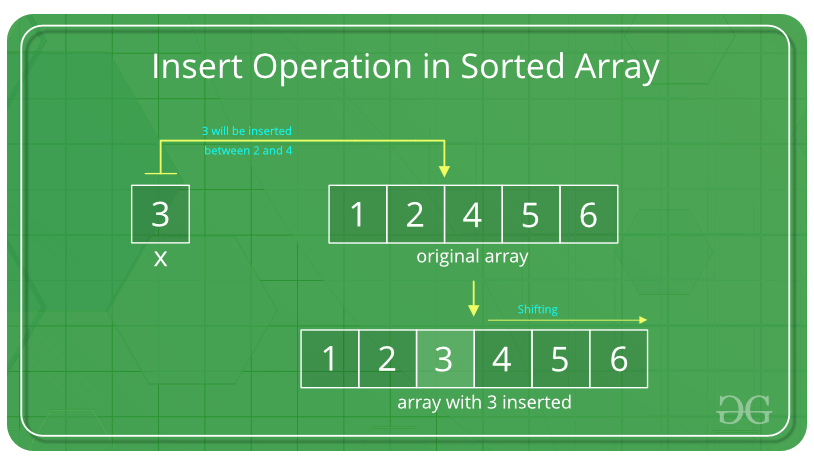
위 영상을 보면 알겠지만,
배열이라는 자료구조에서 빠른 것은 "탐색"뿐이다.
삽입 및 삭제 시에는 기존 데이터들을 이동하는 시간이 걸려서
평균적으로 O(N), 최악의 경우 O(N * log N)이 걸린다.
결국 답은 B-Tree
결국 DB 인덱스로 B-Tree가 적합한 이유는 아래 세 가지다.
실제로 가장 유명한 DBMS 중 하나인 Oracle도 B-Tree를 주로 이용한다.
1. 트리 내 모든 데이터가 항상 정렬된 상태로 유지되기 때문에,
등호(=) 연산뿐만 아니라 부등호(>, <) 연산 처리도 가능하다.
2. 포인터 접근 방식이 적어 매우 많은 데이터가 있어도 속도 이슈가 적다.
3. 데이터 탐색뿐 아니라, 삽입 및 수정 및 삭제에도 항상 O(log N)의 시간 복잡도를 가진다.
(TMI) 그 외 인덱스 자료구조
아래 내용들은 일전에 들은 DB 인덱스 교육 내용 중 일부이며, 그냥 넘어가도 무방하다.
Bitmap
말 그대로, 데이터 뭉치를 비트 열(Bit Array) 형태로 저장하여
이러한 Bitmap에 Bit 연산을 수행하고 DB 인덱스 Value에 대한 RowID를 저장한다.
일반적인 인덱스 자료구조인 B-Tree보다 적은 공간을 차지하며,
B-Tree와 같은 인덱스들은 컬럼의 Cardinality가 높은 경우, 즉, 인덱스하는 값이 반복되지 않는 경우 가장 효율적이라면,
Bitmap 인덱스의 경우, 컬럼의 Cardinality가 "매우" 낮은 경우에 적합하다.
(ex. 고객 DB에서 성별 항목은 보통 남녀 2개의 분명한 값만을 포함)
하지만 DML 작업 시, 성능 저하를 유발하기 때문에 주의가 필요하다.
(데이터 로딩 전 삭제나 작업 완료 후 재생성 동의 방법 등이 필요)
RBO에서는 불가하다.
Function-Based
함수(Function)나 수식(Expression)으로 계산된 결과에 대해 인덱스를 생성하며, 인덱스 형태로 존재하는,
미리 계산되어 있는 결과로 처리한다.
함수나 수식 사용이 반드시 필요하며, 성능 향상을 위해 인덱스가 필요한 경우 적합하다.
하지만 Aggregate Function(SUM, AVG 등)에 대해 적용이 불가하며, RBO에서도 사용이 불가하다.
이 글을 읽으며 B-Tree에 대해 궁금해졌다면,
아래 사이트를 통해 직접 B-Tree를 만들어 볼 수 있다.
(https://www.cs.usfca.edu/~galles/visualization/BTree.html)
그리고 B-Tree에 대해 공부하다 보면 필연적으로 B+-Tree에 대해서도 알게 되는데,
실제로 DB 인덱스로 B+-Tree를 많이 쓴다고도 한다.
역시 아래 사이트를 통해 직접 B+-Tree를 만들어 볼 수 있다.
(https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html)
다음 글은 DB 인덱스 스캔 방식에 대해 알아본다.
끝!
'Study > Database' 카테고리의 다른 글
| [DB] Flyway에 관한 좋은 글 (0) | 2022.02.21 |
|---|---|
| [DB] 인덱스란? - (3) 인덱스 스캔 방식 [개념] (0) | 2021.07.18 |
| [DB] DCL, DDL, DML이란? (0) | 2021.06.02 |
| [DB] 인덱스란? - (1) 개념, 장단점, 쓰는 이유 (0) | 2021.05.31 |
| [DB][MSSQL] PIVOT, UNPIVOT으로 여러 컬럼 합치기 (0) | 2021.04.08 |
거의 모든 DBMS는 인덱스 종류에 대해 특별한 언급이 없다면,
B-Tree 계열 인덱스를 사용하는 경우가 대다수이다.
많고 많은 자료구조에서 왜 하필 B-Tree, B+-Tree를 사용하는지에 대해 알아본다.
이 글을 읽기 전에 이전 글을 읽고 오면 좋으며, 아래 사이트들의 내용을 토대로 작성했다.
- [Naver D2] 성능 향상을 위한 SQL 작성법
- [Tistory] 데이터베이스 인덱스는 왜 'B-Tree'를 선택하였는가
- [Tistory] 인덱스(index)란?
- [Tistory] B-Tree(B트리), B+트리
Tree란?
이 글을 찾아왔다는 것 자체가 Tree에 대한 개념은 이미 알고 있을 것이라 생각하고,
먼저 시간 복잡도에 대해 생각해보자.

일반적으로 위의 그림처럼 평균적으로 생긴 Tree에서 탐색에 대한 시간 복잡도는
O(log N)이다,

하지만, 위의 그림처럼 Tree의 형태가 한쪽으로 추욱 늘어진 최악의 경우엔
O(N)이다.
이러한 최악의 경우를 대비해서 Balanced Tree라는 것을 사용한다.
Balanced Tree?
말 그대로 "균형잡힌 Tree"로,
위에서 본 Tree 구조의 최악의 경우처럼,
트리가 한쪽으로 쏠리지 않게 노드 삽입 및 삭제 시에 특정 규칙에 따라 트리가 재정렬되어
좌 / 우 SubTree의 밸런스를 유지하는 Tree이다.
항상 좌 / 우 SubTree 간에 밸런스를 유지하고 있기 때문에
탐색에 대한 시간 복잡도는 언제나 O(log N)이지만,
노드 삽입 및 삭제 시 발생하는 재정렬 작업 때문에
탐색을 제외한 작업에서는 일반 Tree보다 성능이 좋지 않다.
이러한 Balanced Tree의 예시에는 AVL-Tree, RedBlack-Tree, B-Tree 등이 있다.
왜 하필 (Balanced) Tree를?
Balanced Tree는 최악의 경우에도 탐색 시간이 O(log N)이므로,
탐색 기능 자체만 봤을 때에는 효율적인 자료구조임을 알 수 있다.
하지만 이전 글에서 Hash에 대해 공부하며,
Hash Table이라는 자료구조는 (평균적으로) 모든 자료구조 중 가장 빠른 탐색 시간인
O(1)을 가지는 것을 배웠다.
그렇다면 왜 Hash Table을 쓰지 않고 Balanced Tree를 쓸까?
DB 인덱스가 빠른 데이터 조회를 위해 사용하는 것이라면,
Hash Table을 사용하는 것이 더 효율적인 것 아닐까?
Hash Table의 치명적 단점

Hash Table을 DB 인덱스로 사용할 수 없는 이유에 대해 알아보기 전에
간단하게 개념 먼저 복습하자.
Hash Table은 Hash Function이라는 특정 계산을 하는 함수에 입력 값(keys)이 들어오면
언제나 같은 결과 값(Hash 값)을 내뱉는다.
그리고 이 결과 값은 Hash Table(buckets)의 index 값으로 매핑되어 찾고자 하는 데이터를 얻을 수 있고,
이 과정은 미리 저장된 메모리 공간(Hash Table)에 한 번에 접근을 하기 때문에
O(1)이라는 어떠한 자료구조나 알고리즘보다 빠른 탐색 시간을 갖게 된다.
(물론 Hash 값이 충돌이 일어나는 등의 최악의 경우, O(N)이 될 수도 있다)
이러한 Hash Table의 동작 원리를 머리에 담고,
우리가 DB를 사용할 때 어떤 방식으로 데이터를 조회하는지 생각해보자.
Select CustomerName From Customer Where CustomerID = '2'
위 SQL 쿼리문처럼 조건에 등호(=)만 써서 데이터를 조회했던가?
아니다, "Where CustomerID >= '2'"처럼 부등호도 사용한다.
오히려 이처럼 특정 범위의 값을 조회하는 일이 더 많을 수도 있다.
다시 Hash Table로 돌아오면,
O(1)이라는 탐색 시간은 "단 하나의 데이터를 탐색하는 시간"이다.
그리고 Hash Table에 저장되는 값들은 정렬되어 있지 않기 때문에
특정 값보다 크거나 작은 값을 찾을 수 없다.
혹여 찾을 수 있다 하더라도 O(1) 보다 더 오랜 시간이 걸릴 것이다.
이러한 이유 때문에 DB 인덱스의 자료구조로 Hash Table은 매우 비효율적이어서 잘 사용하지 않고,
Balanced Tree를 사용한다.
그럼 다른 Balanced Tree나 자료구조는?
글 초반부에 Balanced Tree에 대해 설명하며 RedBlack-Tree와 B-Tree를 언급했었다.
두 트리 모두 Balanced Tree이기 때문에
최악의 경우에도 데이터 탐색 시간 O(log N)을 보장하는데,
왜 RedBlack-Tree는 DB 인덱스의 자료구조가 되지 못했을까?
해당 이유에 대해 알아보기 전에 두 트리가 어떤 것인지 간단하게 살펴보자.
RedBlack-Tree?

RedBlack-Tree는 위 그림처럼 각 노드(node)가 하나의 데이터만 가진 상태로
좌 / 우 SubTree의 밸런스를 유지한다.
빨간색(Red)과 검은색(Black) 노드로 구분 지어
노드의 삽입 및 삭제 작업 시, 정해둔 규칙들에 맞게 노드들을 재 정렬하며
AVL-Tree보다는 약간 완화된 버전으로 생각하면 된다.
(더욱 자세한 설명은 위키백과의 글을 참고)
B-Tree?

B-Tree는 위처럼 하나의 노드에 여러 데이터가 저장 가능한 트리이며,
Root - Branch - Leaf의 형태를 갖고 있다.
노드 내의 데이터들은 항상 정렬된 상태이며,
해당 데이터들 사이의 범위를 이용하여 자식 노드를 가질 수 있기 때문에
노드 내 데이터의 개수가 N개일 때, 자식 노드의 개수는 (N + 1) 개다.
DB 인덱스를 B-Tree로 구성할 경우,
가장 아래의 Leaf Node에 인덱스 Value에 대한 RowID를 저장한다.
(TMI)
인덱스를 구성하는 컬럼의 Cardinality가 높은 경우, 즉, 중복된 값의 Row가 적은 비율을 가지는 컬럼,
다시 말해, 컬럼의 분포도가 10~15% 이내인 경우 적합하다.
RedBlack-Tree의 치명적 단점
위 그림들만 봐도 알 수 있듯이,
RedBlack-Tree와 B-Tree의 가장 큰 차이는 '하나의 노드 내의 데이터 개수'이다.
RedBlack-Tree는 하나의 노드 내에 무조건 하나의 데이터만을,
B-Tree는 하나의 노드 내에 여러 데이터를 저장할 수 있다.
이러한 데이터 저장 방식의 차이는 어떤 차이를 일으킬까?
바로 "데이터 탐색 시의 속도 차이"다.
Tree 자료구조에서 데이터를 탐색할 때에는,
가장 위에 있는 root 노드부터 시작하여 찾는 데이터가 나올 때까지
자식 노드로 내려가며 탐색한다.
RedBlack-Tree의 구조를 보면 하나의 노드에 하나의 데이터만 있기 때문에
자식 노드로 넘어가는 횟수가 많을 것이고,
그러한 노드와 노드 사이는 "참조 포인터(reference pointer)"로 연결되어 있다.
하지만 B-Tree의 경우,
하나의 노드 내에 정렬된 데이터들이 마치 "배열"의 모습을 띄고 있는데
실제 메모리 상에 배열처럼 차례대로 저장이 되어있다.
컴퓨터 공학 관련 과목이나 공부를 해본 사람이라면,
포인터로 메모리에 접근 시 CPU 연산을 통해 주소를 알아내는 등의 부가적인 연산이 필요하기 때문에
실제 메모리 디스크에서 바로 다음 인덱스로 접근을 하는 배열 방식이
포인터 접근을 하는 것보다 훨~씬 빠르다는 것을 알 것이다.
물론, 이론적인 시간 복잡도는 두 트리 모두 O(log N)이지만
위와 같은 물리적인 메모리 처리에서 퍼포먼스 차이는 배열 구조의 접근 방식이 굉장히 빠를 수밖에 없다.
데이터 개수가 무의미할 정도로 적다면 상관없겠지만,
유의미할 정도로 많은 개수를 다룬다면 큰 차이가 있을 것이다.
(참고 - B-Tree 시간 복잡도 계산)
B-Tree에서 시간 복잡도를 계산할 때,
노드들 간 탐색 시간인 O(log N)과 하나의 노드 내 데이터를 탐색하는 시간인 O(log M)을
따로 계산해야 하는지 의문이 생길 수 있다.
하지만, 일반적으로 B-Tree는 하나의 노드에 저장될 노드 개수를 상수로 제한하기 때문에
시간 복잡도 계산에서 제외된다.
그럼 배열을 쓰면 되지 않나?
RedBlack-Tree를 사용하지 않는 이유가 포인터 접근 방식으로 인한 속도 이슈 때문이라면,
아예 배열을 DB 인덱스로 사용하면 되지 않을까?
응, 아니다.
배열의 치명적 단점

배열에 대한 설명은 최근 올라온 유튜브 영상(링크)으로 대체한다.
노마드 코더로 유명한 니콜라스 님의 12분짜리 배열 설명 영상인데
말씀하시는 속도가 느려서 2배속으로 봐도 충분하다.

위 영상을 보면 알겠지만,
배열이라는 자료구조에서 빠른 것은 "탐색"뿐이다.
삽입 및 삭제 시에는 기존 데이터들을 이동하는 시간이 걸려서
평균적으로 O(N), 최악의 경우 O(N * log N)이 걸린다.
결국 답은 B-Tree
결국 DB 인덱스로 B-Tree가 적합한 이유는 아래 세 가지다.
실제로 가장 유명한 DBMS 중 하나인 Oracle도 B-Tree를 주로 이용한다.
1. 트리 내 모든 데이터가 항상 정렬된 상태로 유지되기 때문에,
등호(=) 연산뿐만 아니라 부등호(>, <) 연산 처리도 가능하다.
2. 포인터 접근 방식이 적어 매우 많은 데이터가 있어도 속도 이슈가 적다.
3. 데이터 탐색뿐 아니라, 삽입 및 수정 및 삭제에도 항상 O(log N)의 시간 복잡도를 가진다.
(TMI) 그 외 인덱스 자료구조
아래 내용들은 일전에 들은 DB 인덱스 교육 내용 중 일부이며, 그냥 넘어가도 무방하다.
Bitmap
말 그대로, 데이터 뭉치를 비트 열(Bit Array) 형태로 저장하여
이러한 Bitmap에 Bit 연산을 수행하고 DB 인덱스 Value에 대한 RowID를 저장한다.
일반적인 인덱스 자료구조인 B-Tree보다 적은 공간을 차지하며,
B-Tree와 같은 인덱스들은 컬럼의 Cardinality가 높은 경우, 즉, 인덱스하는 값이 반복되지 않는 경우 가장 효율적이라면,
Bitmap 인덱스의 경우, 컬럼의 Cardinality가 "매우" 낮은 경우에 적합하다.
(ex. 고객 DB에서 성별 항목은 보통 남녀 2개의 분명한 값만을 포함)
하지만 DML 작업 시, 성능 저하를 유발하기 때문에 주의가 필요하다.
(데이터 로딩 전 삭제나 작업 완료 후 재생성 동의 방법 등이 필요)
RBO에서는 불가하다.
Function-Based
함수(Function)나 수식(Expression)으로 계산된 결과에 대해 인덱스를 생성하며, 인덱스 형태로 존재하는,
미리 계산되어 있는 결과로 처리한다.
함수나 수식 사용이 반드시 필요하며, 성능 향상을 위해 인덱스가 필요한 경우 적합하다.
하지만 Aggregate Function(SUM, AVG 등)에 대해 적용이 불가하며, RBO에서도 사용이 불가하다.
이 글을 읽으며 B-Tree에 대해 궁금해졌다면,
아래 사이트를 통해 직접 B-Tree를 만들어 볼 수 있다.
(https://www.cs.usfca.edu/~galles/visualization/BTree.html)
그리고 B-Tree에 대해 공부하다 보면 필연적으로 B+-Tree에 대해서도 알게 되는데,
실제로 DB 인덱스로 B+-Tree를 많이 쓴다고도 한다.
역시 아래 사이트를 통해 직접 B+-Tree를 만들어 볼 수 있다.
(https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html)
다음 글은 DB 인덱스 스캔 방식에 대해 알아본다.
끝!
'Study > Database' 카테고리의 다른 글
| [DB] Flyway에 관한 좋은 글 (0) | 2022.02.21 |
|---|---|
| [DB] 인덱스란? - (3) 인덱스 스캔 방식 [개념] (0) | 2021.07.18 |
| [DB] DCL, DDL, DML이란? (0) | 2021.06.02 |
| [DB] 인덱스란? - (1) 개념, 장단점, 쓰는 이유 (0) | 2021.05.31 |
| [DB][MSSQL] PIVOT, UNPIVOT으로 여러 컬럼 합치기 (0) | 2021.04.08 |
